三态电路
三态电路是一种很重要的总线接口电路,在数字系统中得到了广泛的应用。
所谓“三态”,是指正常0态、正常1态和高阻态Z。
其中,前两种状态的输出阻抗很低,所以又称为低阻0态和低阻1态。而高阻态是指三态电路的输出呈高阻。
多个三态电路的输出可以连接在一起去驱动总线。当接在总线上的三态电路输出为高阻态时,电路在形式上是和总线相连的,但实际上可以看成是和总线“脱开”的。
高阻态简称 Z 态。
三态门有两种:
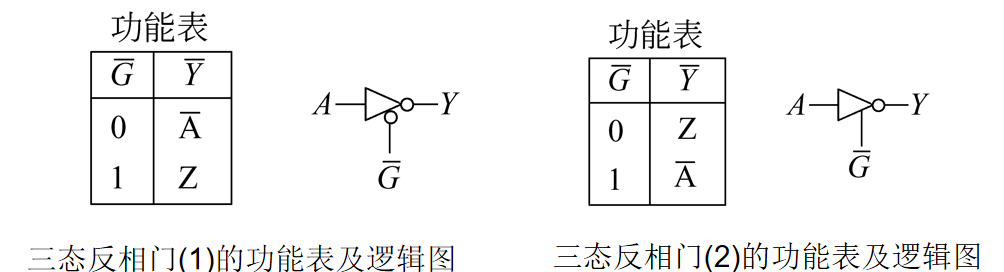
其中(1)是低电平有效,(2)是高电平有效。
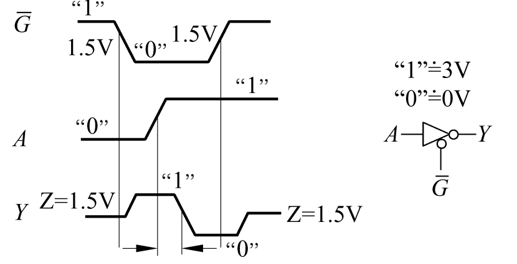
若干个三态门共同驱动总线式最常见的应用。在时序图中通常用“不高不低”的“中间线”来表示Z态,数据输入和输出有上升延迟和下降延迟。
当总线传送数据时应该只有一个三态门处于正常态,其余的三态门均应处于高阻态。
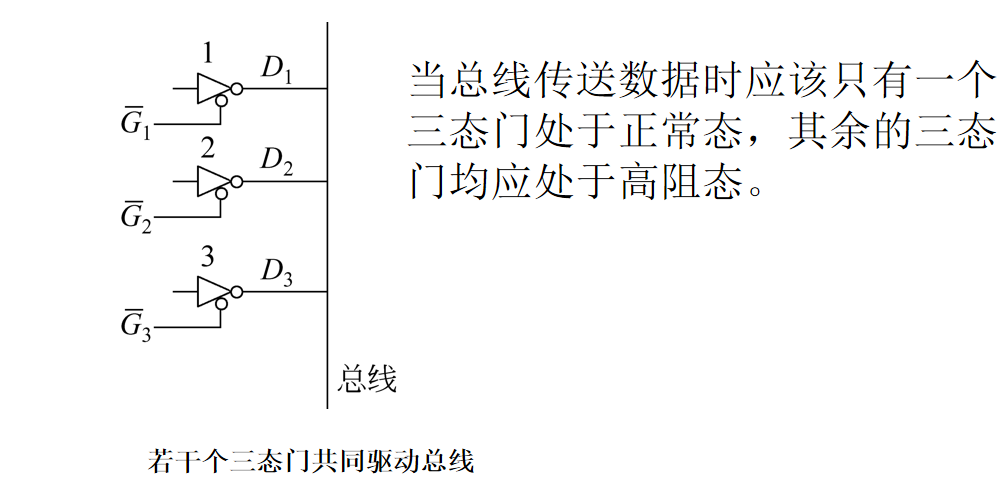
为了防止出现多个三态门与总线相通的情况,三态电路由正常态转变为高阻态的过程总是快于高阻态向正常态的转变的。这样,即使G2的负跳变和G1的正跳变同时到来,也不能出现门1和门2同时处于正常态的情况。
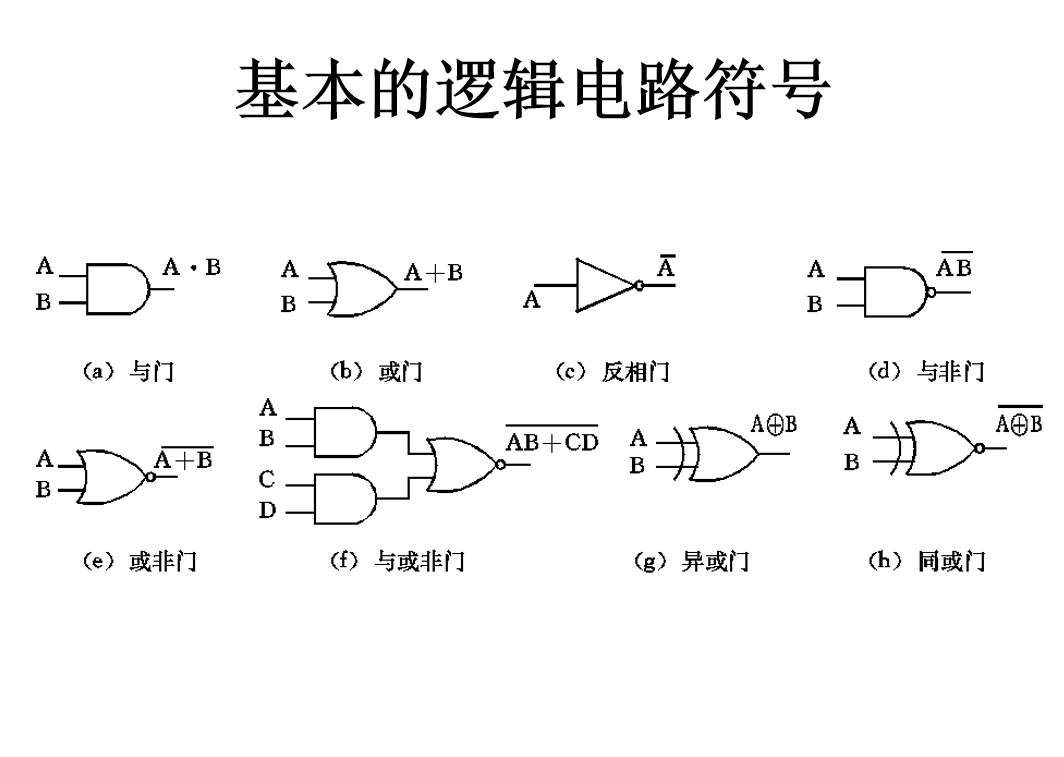
基本的逻辑电路符号
异或门及其应用
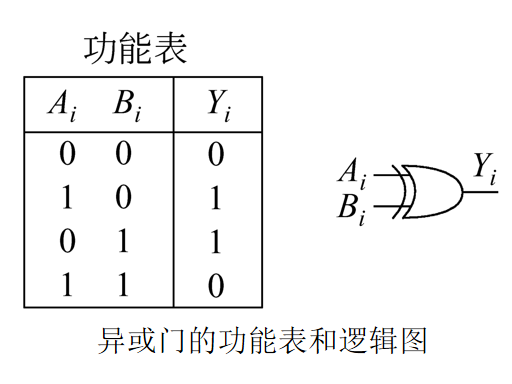
异或:简单的的说就是,相同为0,不同为1.
在计算机中,异或门主要有如下应用:
半加器
数码比较器
奇偶校验电路
异或还具有如下特性:
A ^ 0 = A; // 原码输出
A ^ 1 = ~A; // 反码输出故它还可以用作原/反码输出电路的设计当中
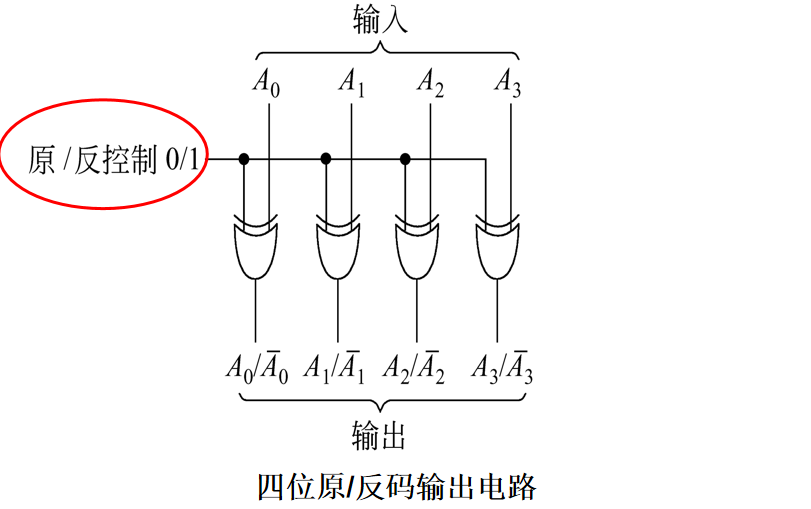
在半加器中,异或的运算完美契合了半加,也即不带进位的运算规则,可以说,一个半加器其实就是一个异或门。
在比较器中的用途,如下
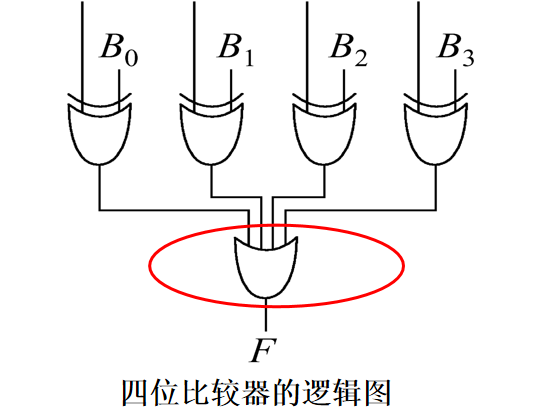
将上述电路图转换为公式后,如下:
F = (A0 ^ B0) + (A1 ^ B1) + (A2 ^ B2) + (A3 ^ B3)当每一位都相同时,F 输出为 0 ,只有至少有一位不相同,则 F 输出为 1
在奇偶检测电路中,异或门的应用如下:
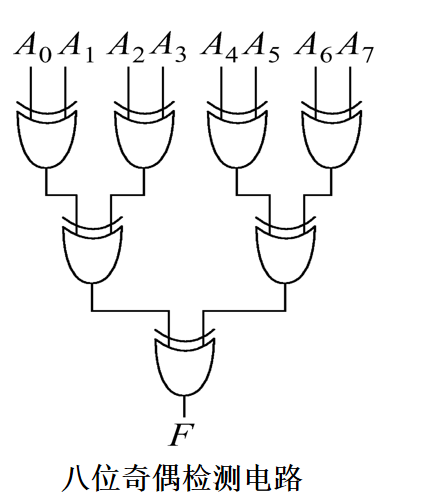
F = A0 ^ A1 ^ A2 ^ A3 ^ A4 ^ A5 ^ A6 ^ A7 ^ A8;当 8 位中包含奇数个 1 时, F = 1, 否则, F = 0;
在奇偶校验电路中,校验码由数据位和一位校验位共同组成。
奇校验要求添加校验位后,数位中 1 的个数为 奇数,也即所有数的异或和应该为 1
偶校验要求添加校验位后,数位中 1 的个数为 偶数,也即所有数的异或和应该为 0
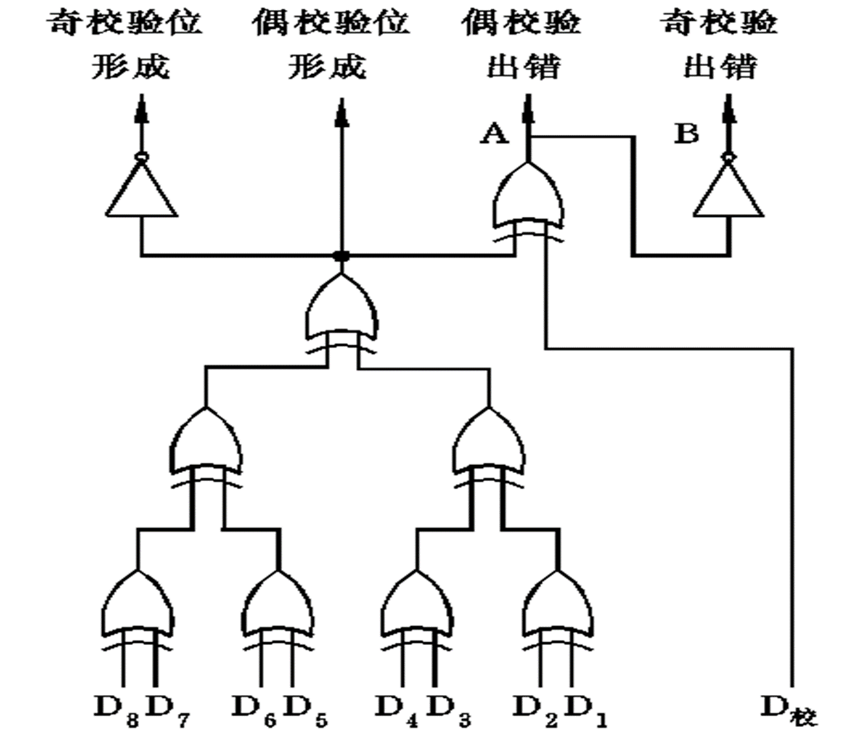
校验的原理,本质上就是通过异或操作,将接受到的数据再进行异或求和,若传输没有差错,则其值应该与传送前的数据异或和相同,也即二者再取异或的值应该为0。若为 1,则说明在传输过程中发生了差错。
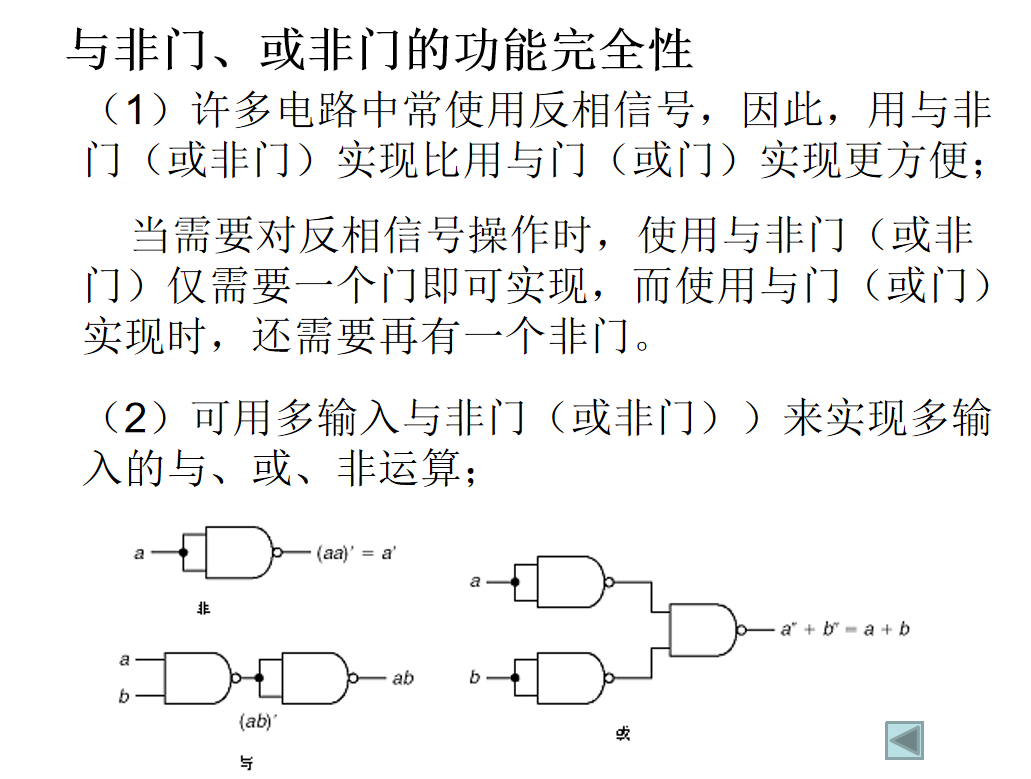
除此之外,异或门之所以如此受大家青睐,很大的原因就是它能够起到简化电路设计的功能。
运算器

运算器部件是计算机中的执行部件,它可以对二进制数据进行各种算术和逻辑运算;
在运算器中,为了避免频繁地访问存储器,在运算器内部还设定了若干的通用寄存器,构成了通用寄存器组。
寄存器组越多对提高运算器的性能和程序执行速度就越有利。
其中,有一类通用寄存器是用来提供一个操作数并存放运算结果的,也就是累加器Acc(Accumulator)。累加器可以有一个,也可以有多个。
还有一些专用寄存器,用于记录程序执行过程中的重要状态,如程序字PSW、堆栈指针SP等。这些专用寄存器,有一些,比如说循环计数器,对程序员来说,是透明的,程序员可以通过指令来使用它,而用户是不能访问的。
除了这些寄存器之外,运算器中还附加了一些控制电路,例如,二进制中的移位操作就是通过在ALU的输出端设置移位电路来实现的,移位电路也就是一个多路选择器,包括左移,右移,直送三种操作。
加法器
半加器
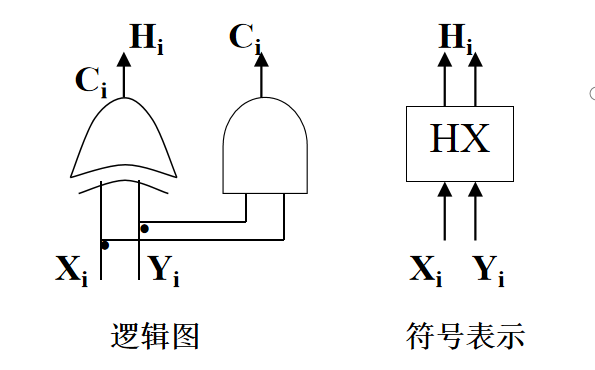
两个一位二进制数相加,不考虑低位进位,用一个简单的异或门即可实现。
进位产生 Ci = Xi * Yi
本位 Hi = (~Xi) * Yi + Xi * (~Yi)全加器
两个一位二进制数相加,不仅考虑本位,还考虑低位的进位。
其真值表如下:
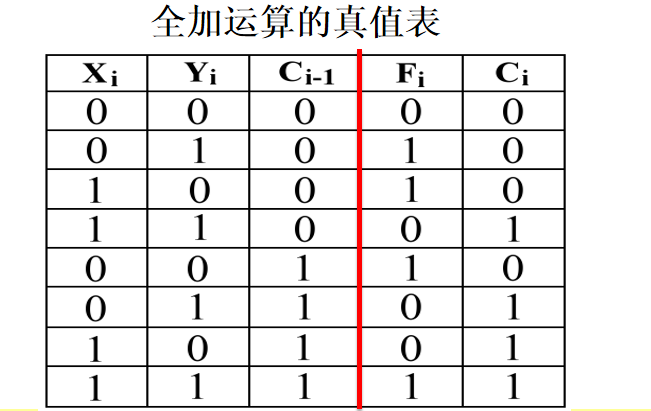
逻辑表达式,本质上就是离散数学中的主析取范式,对应到门电路图中也是同理,将各种所有可能的合法情况聚合到一起,然后析取,最后再通过离散数学中的相关逻辑运算可达到简化式子的目的。
j = i - 1;
k = j + 1;
本位 Fi = (~Xi)Yi(~Cj) + Xi(~Yi)(~Cj) + (~Xi)(~Yi)Cj + XiYiC = Xi ^ Yi ^ Cj
进位 Ck = XiYi(~Cj) + (~Xi)YiCj + Xi(~Yi)Cj + XiYiCj = (Xi ^ Yi)Cj + XiYi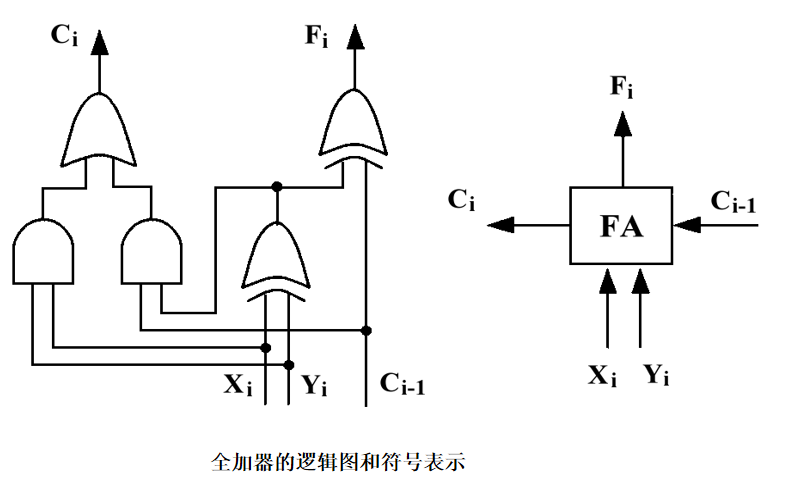
加法器
要实现 N 位二进制数的相加,就需要组成加法器。最基本的加法器有如下两种:
串行加法器
并行加法器
在进行加法运算时,由于一位全加器只能实现两个一位二进制数的运算,而门电路都会有延迟,这就会影响整个加法器的运算速度,若要做优化,则可从这入手。
串行加法器
n 位字长的加法器,仅用一位全加器,通过移位寄存器从低位到高位串行地提供操作数,分 n 步进行相加的,即为串行加法器。
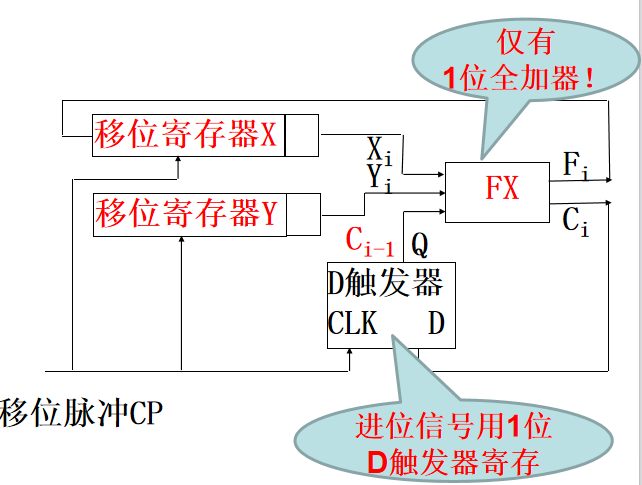
完成两个 n 位二进制数的相加, 共需要 n 步加法, n 步移位,速度太慢,现代计算机几乎不再采用。
并行加法器
与串行加法器相比,最大的区别之一就是用到了多个全加器。
并行加法器全加器的个数与机器字长相同,能同时对所有位求和。
它的最长运算时间主要取决于两部分:
全加器本身求和的延迟时间 、 进位信号的传递时间。
全加器本身求和的延迟时间无法改变,故若考虑优化的话只能从进位的产生与传递入手。
在全加器的进位链结构中,最基本的有如下两种:
串行进位
并行进位
在这一基础上,又可以将全加器进行分组、分级,对组内、组间、级间分别采用串行进位和并行进位。
将 n 个全加器串联在一起即可得到串行进位加法器,这种结构的加法器,从低位传来的信号是逐位向高位串行传播的,所以,这种加法器也叫,行波进位加法器。
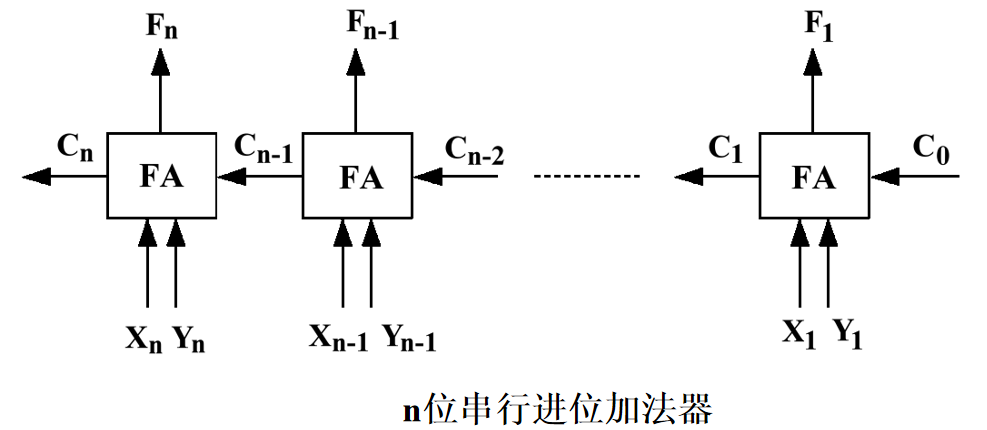


假设一级与非门(或非门)的延迟时间是1ty,与或非门的延迟时间为1.5ty,因此产生进位C1延时时间2.5ty,于是得到最长进位延迟时间为2.5nty,与n成正比。
行波进位加法器的加法速度比较低。
之所以慢,本质上是因为进位产生与传递的速度太慢了,高位加法器需要等待低位加法器的进位信号。
接下来,我们看看并行进位加法器。
前面提到了,提高加法器的运算速度的关键是消除行波进位中的进位逐位串行传播,让各位进位独立地同时形成。
则将之前串行进位的公式,进行逐级推导后,可得如下:
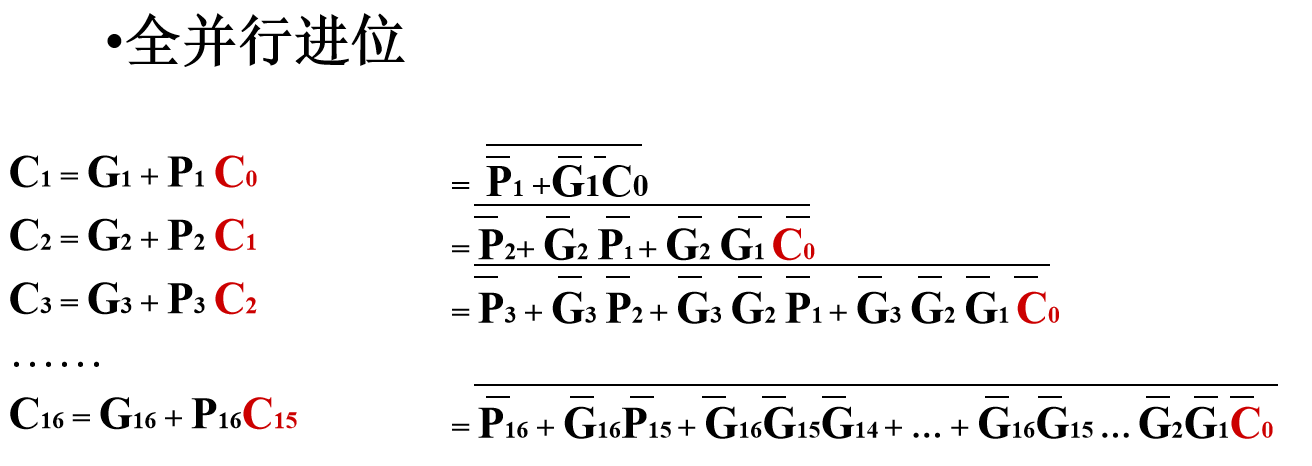
可以看到,只要知道 进位产生函数Gi、进位传递Pi、和最低进位C0,就可以快速求得本位向高位的进位信号,而 Gi 与 Pi, 我们可以通过取两个二进制数的相应位的操作数快速获得,C0则是一开始就知道的。
所以,理论上而言,整个加法器的耗时,只有全加器本身求和的延迟时间。假设产生进位的延时时间为 2.5ty, 则只需要 2.5 ty 的时间就可以完成全部二进制数的运算。
但我们也应该注意到,上述式子展开,越往后,其逻辑表达式就越长,所要设计的相应的门电路也变的越来越复杂,所以这只能在理论中想想就行,在现实工程中还要考虑到电路设计的复杂程度及其花销。
所以,一个调和折中的做法就是,在保证快速进位的同时,减少电路的复杂性,比如,以四个全加器作为一组,在组间再分别进行串行进位或并行进位。
组内并行,组间串行(单级先行进位)
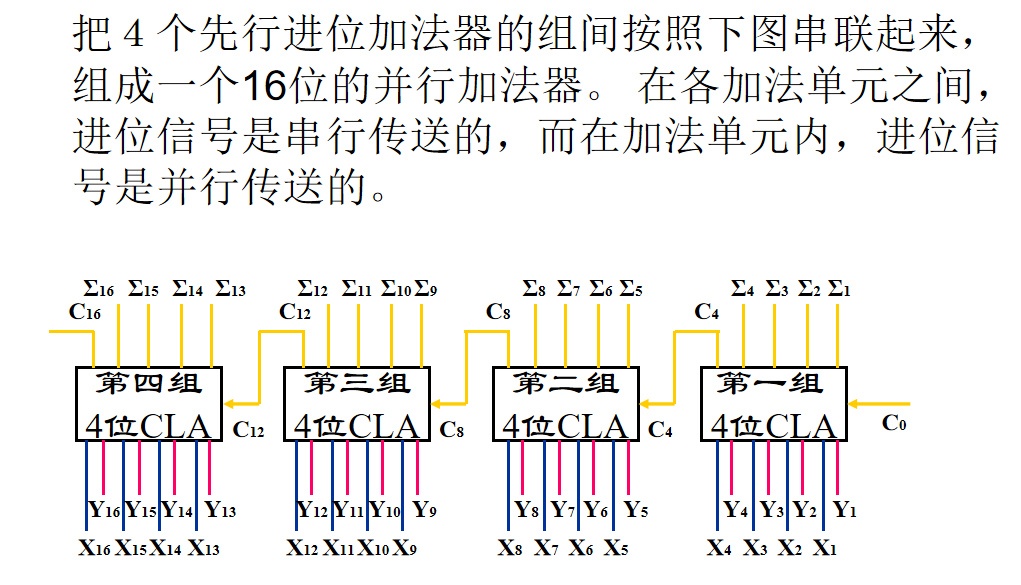

可以看到,每一组间的运行规则,只同该组内的最低进位,和可快速求得的 Gi, Pi 有关,而组间则采用串行进位,需要等低位组算完后,产生进位信号传递给高位组。
组内并行,组间并行(多级先行进位)
对于多级先行进位而言,为了实现组间的并行运算,还引入了组间的进位传递函数G(Ⅰ,Ⅱ,Ⅲ,Ⅳ) 和进位产生函数 P(Ⅰ,Ⅱ,Ⅲ,Ⅳ)

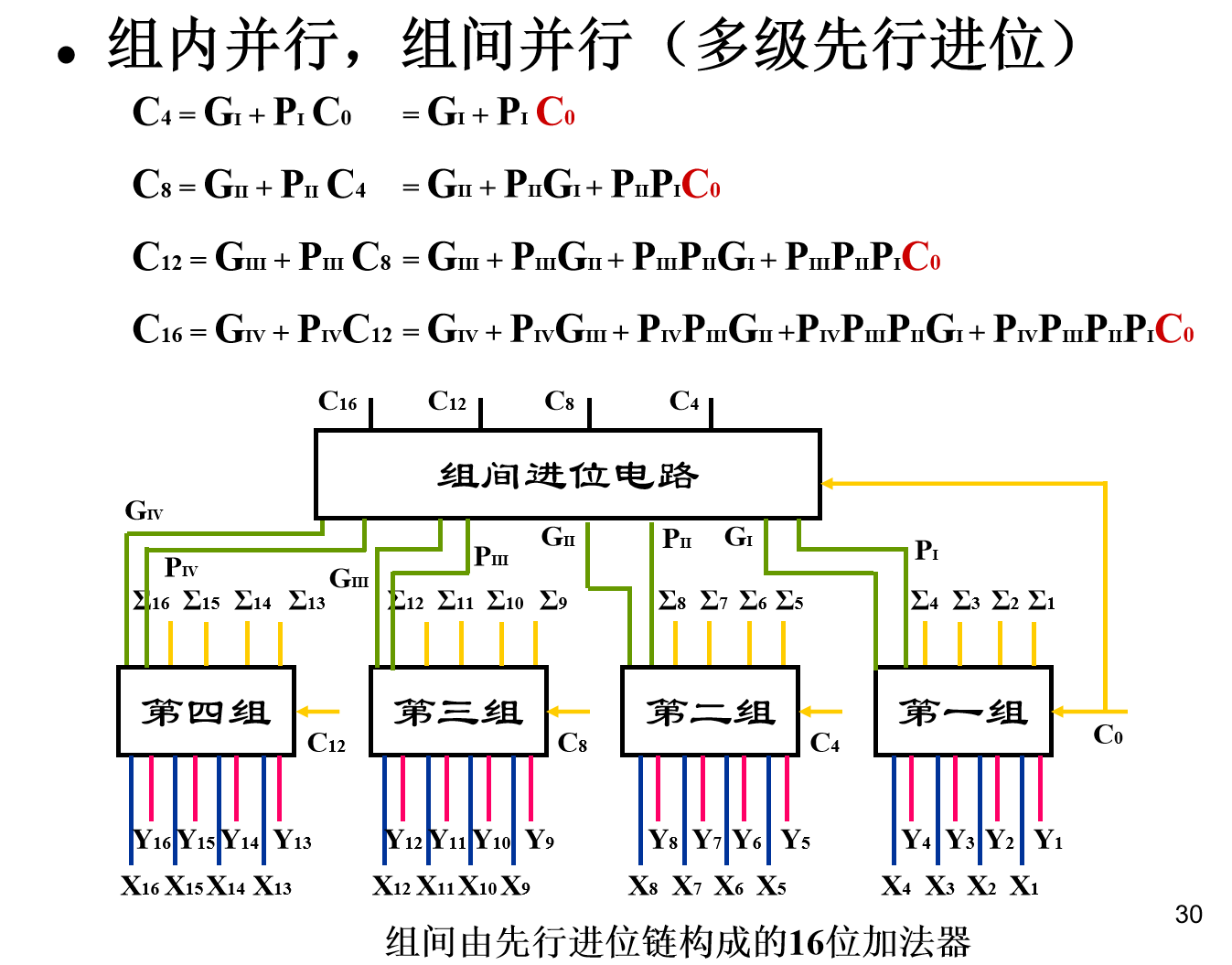
组间的并行进位与组内的并行进位其实逻辑上是等价的,唯一的区别,可能就是,对于组间进位而言,其进位的位权要更大一些而已。
好了,至此加法器这一篇章的内容,我们就全都搞定辣~


