数据的表示和转换

数据的表示可以用如下的图片简单概括：

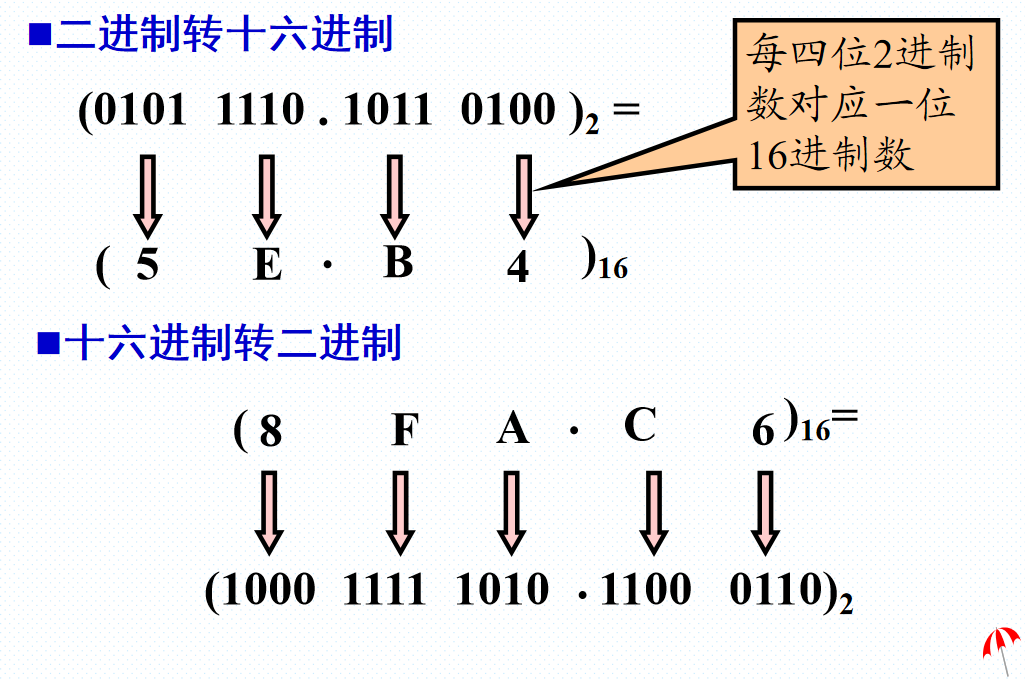
各进制间的转换关系如下：

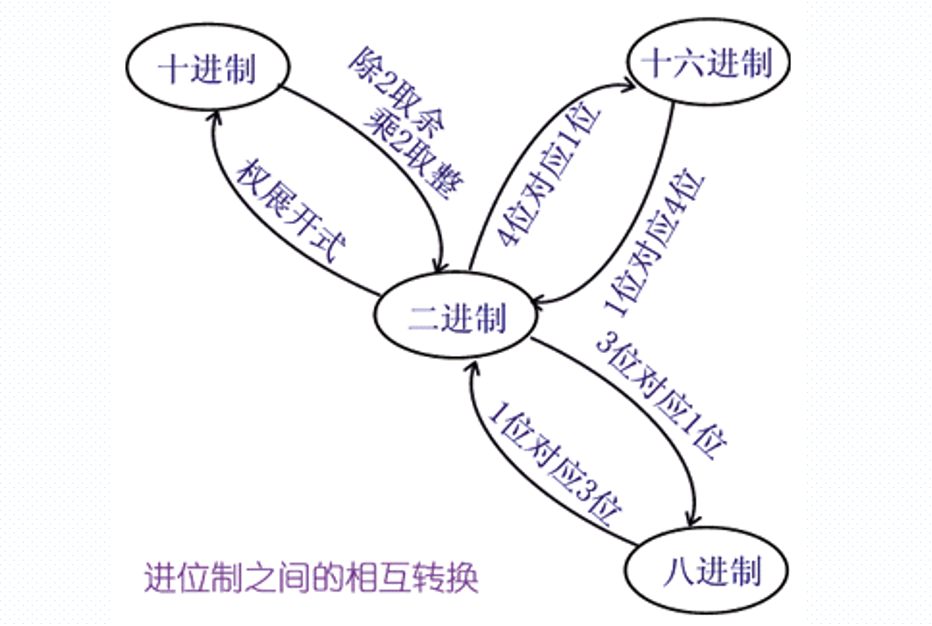
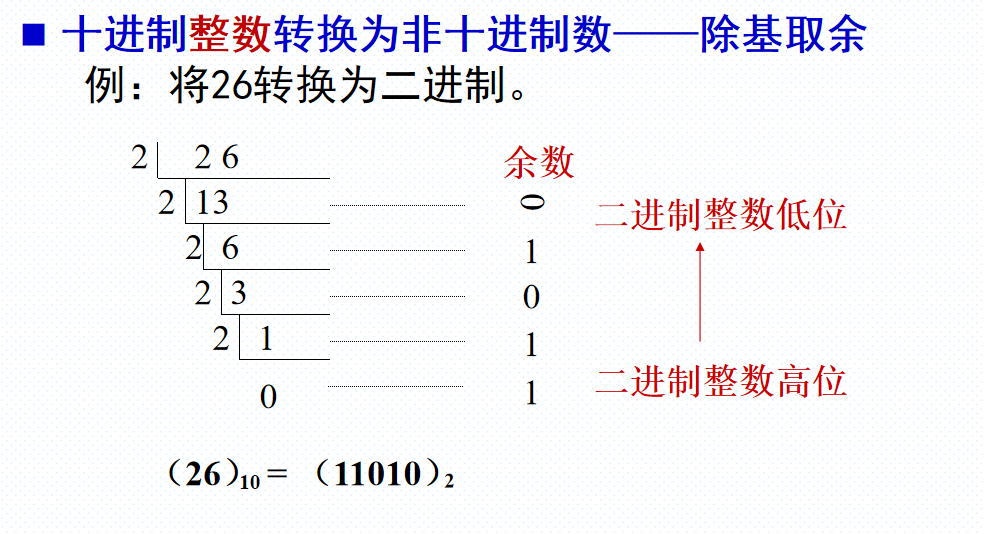
乘基取整法:直到乘积小数部分为0或已满足所要求的精度为止。

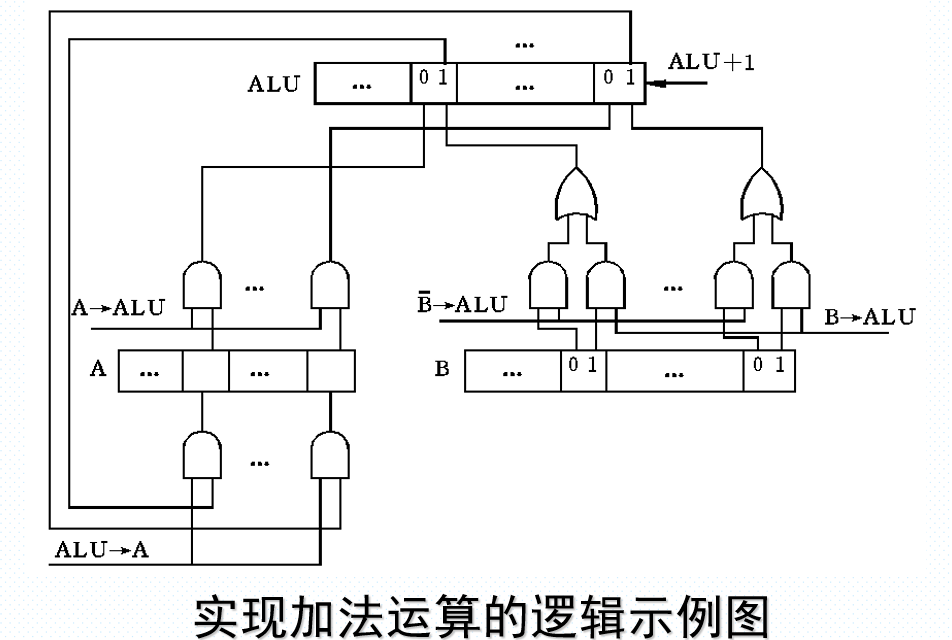
十进制数的编码与运算

对于8421码

在某些情况下，当使用8421码进行加法或减法运算时，可能会得到超出正常十进制表示范围的结果。这时，就需要进行修正以确保结果的准确性。

对于加法运算，当得到的结果处于1010-10010（即十进制中的10-18）这个非法区间内时，需要进行修正。修正的方法是加上0110（即十进制的6），然后高位补0以凑足8421码。例如，如果你得到的结果是1101（即十进制的13），这是一个无效的状态，因为1101在8421码中没有对应的十进制数。因此，你需要进行修正：1101 + 0110 = 0001 0011，这个结果（0001 0011）就是修正后的8421码，对应的十进制数是19。

对于减法运算，如果在某一位的减法中，被减数小于减数，就需要从高位借位。但请注意，在8421码中，借位的处理方式与常规二进制有所不同。由于8421码是基于十进制的，所以借位时不是简单的借“1”，而是相当于借“10”（在十进制中）。然而，由于我们是用二进制表示的，所以实际操作中，我们需要借“16”（在二进制中表示为10000）然后减去“6”（在二进制中表示为0110）。这意味着，当我们需要从高位借位时，我们需要在低位加上0110来进行修正。

如果结果超出了有效范围，但仍在1010-10010（对应十进制中的10-18）之间，可以通过加上0110（即十进制中的6）并高位补0来进行修正。例如，如果结果是1101（即十进制中的13），则修正为0001 0011（即十进制中的19）

计算机中的二进制数表示

原码表示法

补码表示法

减法运算也可以通过补码来间接进行运算：

反码表示法

移码表示法

四种机器数表示方式比较

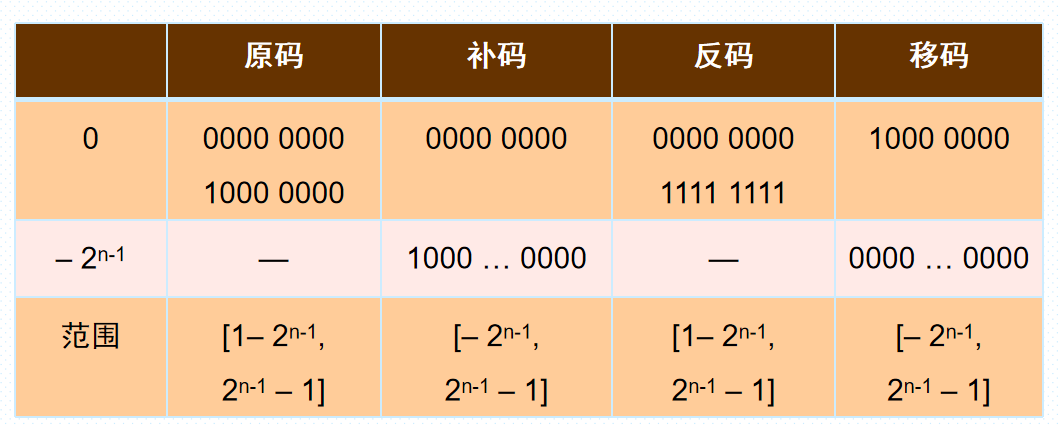
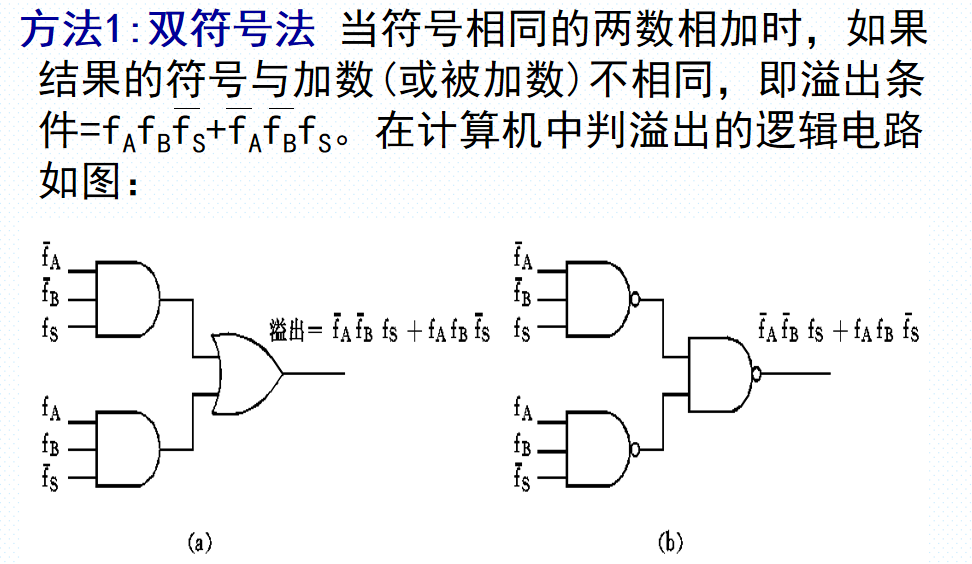
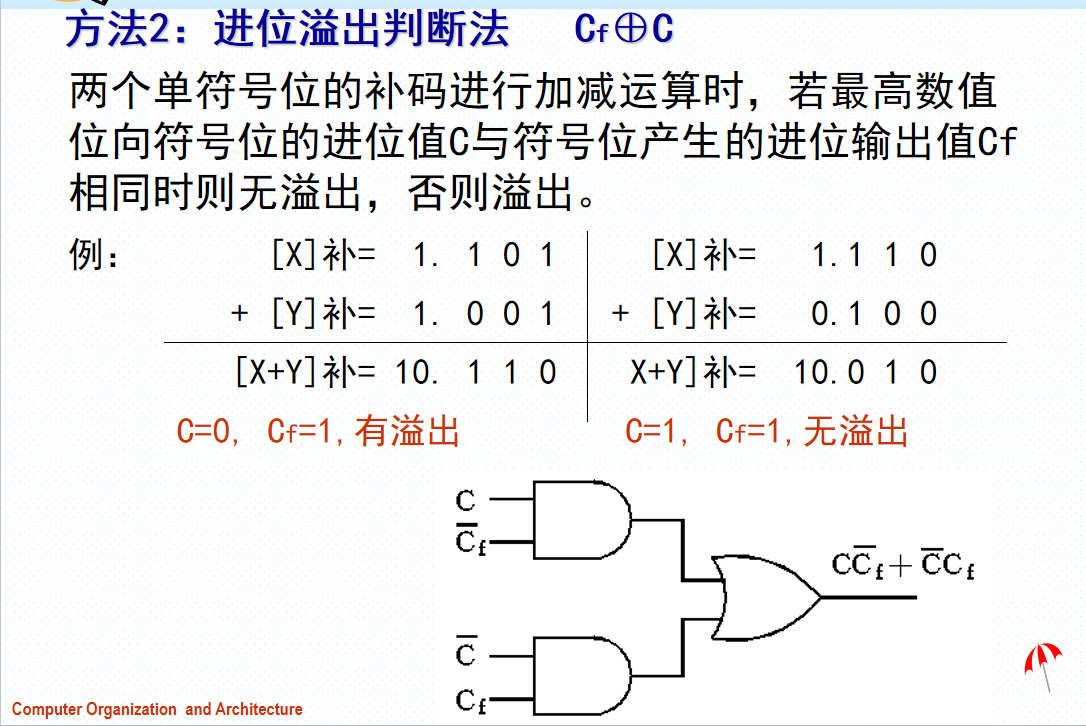
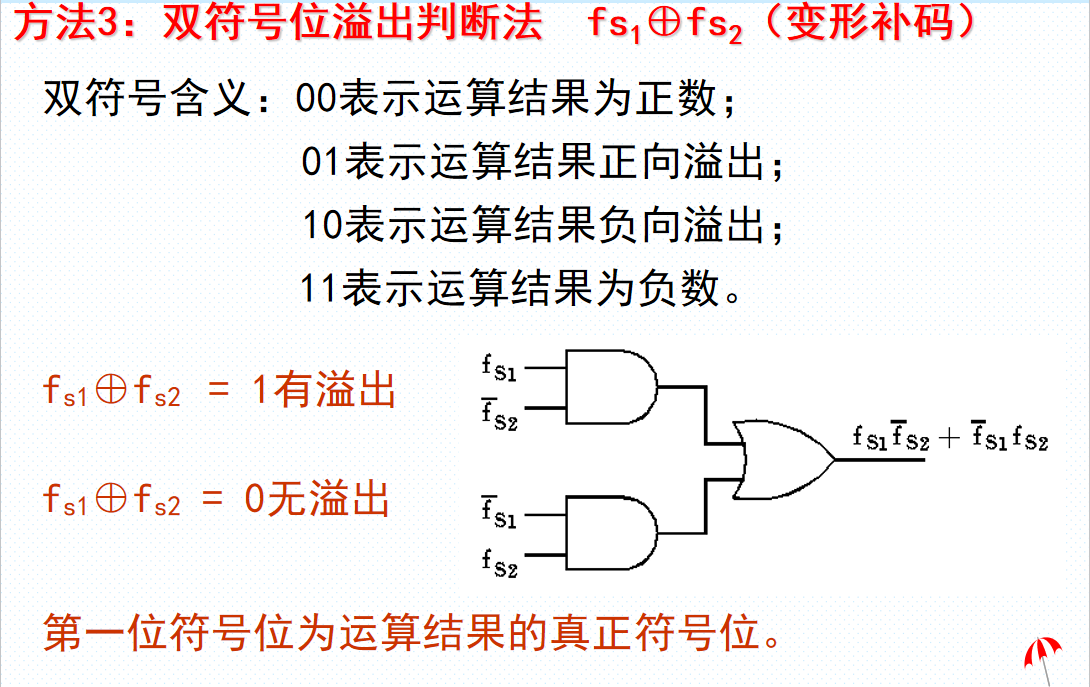
定点数加减溢出

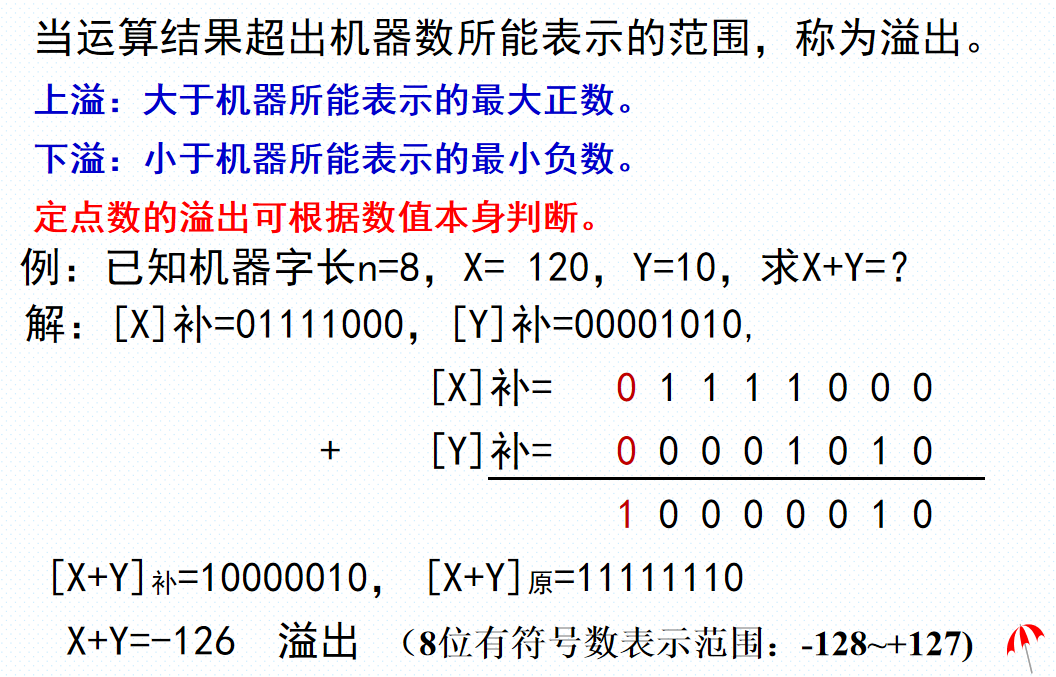
溢出判断规则

溢出判断方法