校验码是具有发现错误或修正错误能力的数据编码。
校验的原理概括的说,是假设被校验数据(原始数据)字长为M位,引入部分冗余信息(校验数据)K位,使得最终的校验码(原始数据+校验数据)符合某种编码规则。当校验码中某些位出现错误时,会破坏预定规则,从而使得错误被检测,甚至被纠正。
校验码的引入是为了解决编码在时间、空间上传输可靠性的问题。
最小码距(Minimum Distance)是编码理论中的一个重要概念,它指的是在给定的编码集合中,任意两个不同编码之间对应位上编码不同的位数的最小值。最小码距是衡量编码性能的一个重要指标,它与编码的纠错能力密切相关。
具体来说,最小码距越大,编码的抗干扰能力越强,纠错能力也越强,但相应的数据冗余度也会增加,编码效率可能会降低。因此,在设计编码方案时,需要综合考虑最小码距的大小和编码效率,以确保编码的可靠性和有效性。
检验码引入冗余的过程实际上就是增加最小码距的过程。
码距与检错、纠错能力之间的关系
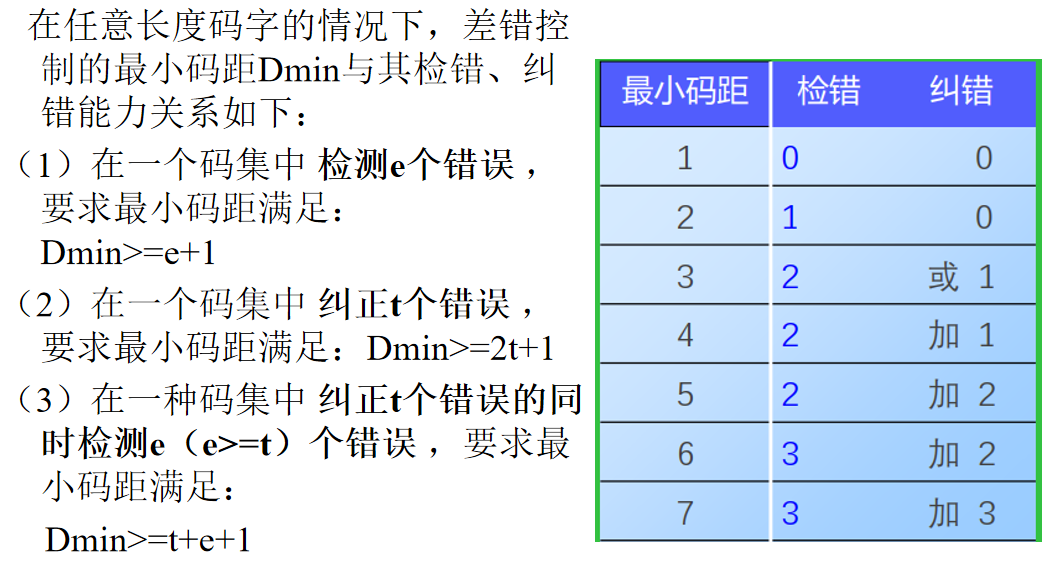
若码距 d 为奇数,可以发现 d - 1 位错误,可以纠正 (d - 1)/ 2 位错误
若码距 d 位偶数,可以发现 d / 2 位错误, 可以纠正 d / 2 - 1 位错误
下面来看看几种常见的校验码。
奇偶校验码
奇偶校验码是由若干位数据位加一位校验位共同组成的。
奇校验:使得整个校验码中 “1” 的个数为奇数
偶校验:使得整个校验码中 "1" 的个数为偶数

奇偶校验码的码距为 2, 可以发现一位错(奇数位错), 不能检查偶数位错,且不具备纠错能力。
具体电路设计图如下:

一般在同步传输方式中常采用奇校验,异步传输方式中常采用偶校验。
海明校验码
海明码不仅能够发现出错,还具备一定的纠错能力,其本质可以看成多组偶校验的共同组合。
海明码由若干位校验位和数据位共同组成,按照其检错、纠错能力可划分为如下两种海明码
检1纠1海明码

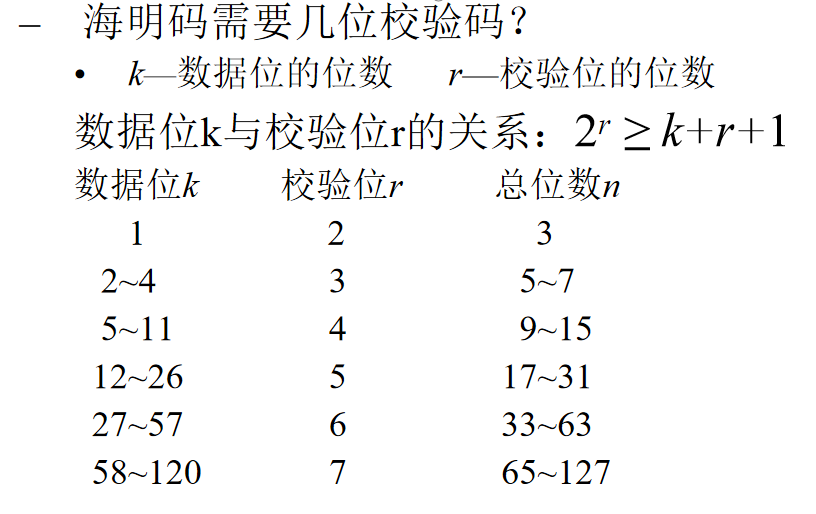
确定海明码的位数,规则如下:
那么海明码具体要如何编码呢?下面我们结合一个例子来给大家说明一下:
eg. 假设要传输的数据为 10101100,请确定由它生成的海明码。
数据位 k = 8, 由海明不等式 2r >= k + r + 1, 可得共需要4位校验位。
则校验码共有 8 + 4 = 12 位,假设从低到高,每一位的位号为 Hi (i = 1, 2, 3, ... 12)。
则具体来说,校验位 P 和 数据位 D 同位号以及校验的对应关系如下图。
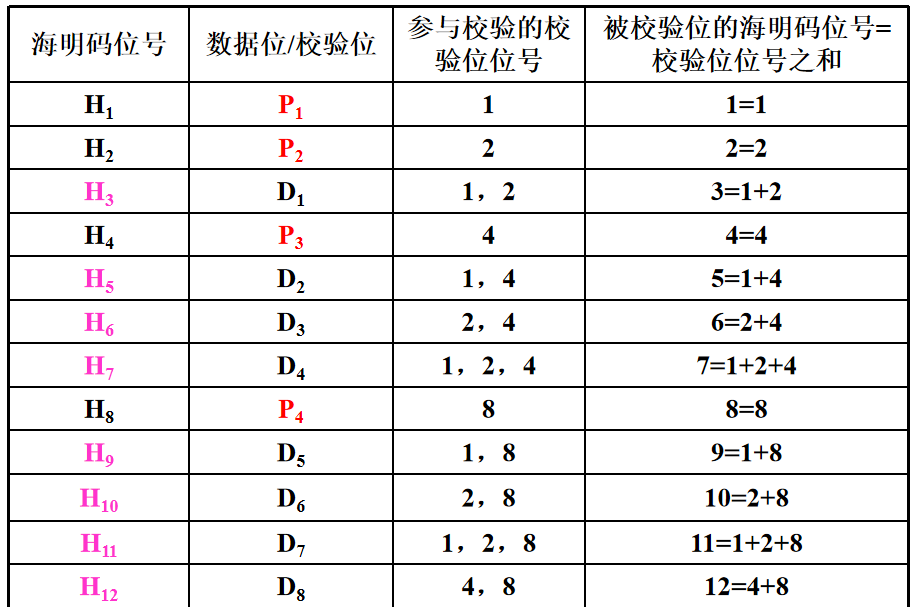
由上表我们可以得到如下信息:
海明码的校验位并不是连续排列的,而是放到了校验码中第 1, 2,... 等 2 次幂位或者最高位上(当最高位不是2次幂时)。
海明码本质上是多个偶校验的组合,故校验位的确定也遵循偶校验的原则,只不过不同于偶校验的一点,在于校验的数据位并不是全体校验码,而都是校验码的一部分。具体来说,对于8 + 4的海明校验,符合如下的规则,P1 负责 H1, H3, H5, H7, H9, H11, P2负责H2,H3, H6,H7,H10,H11, P3负责H4,H5,H6,H7, H12,H13,P4负责H8,H9,H10,H11,H12。
分析上述各校验位管辖的位号,可以得出结论:从低到高来看,第一位校验位的管辖范围为,从该校验位的位号开始,选一隔一,第二位校验位的管辖范围为,从该校验位的位号开始,选二隔二,第三位校验位的管辖范围为,选三隔三,第四位校验位的管辖范围为选四隔四。
如果再从位号来分析的话,对于每一位位号,其受管辖的校验位的位号其实就是这一位的二进制表示,比如说,对于H11而言,其二进制表示为 1 + 2 + 8,则这一位就受 H1,H2,H8,这三个校验位的管辖。
则回到刚才的例子,10101100的海明码表示格式应该是如下格式
1010P4110P30P2P1

相信看到这里,对于检1纠1的海明码,你应该就问题不大了。
对于检1纠1的海明码,其电路设计图如下:
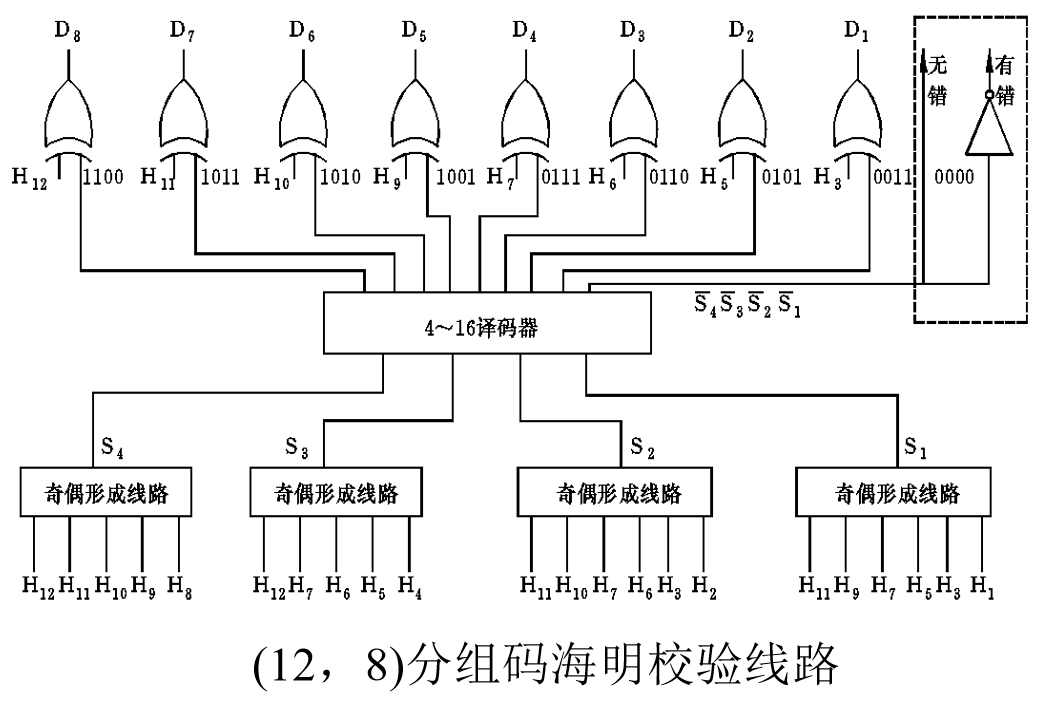
对于检1纠1的海明码,由于每一个校验位仅负责部分校验码的检验,且使用的是偶校验原则,所以对于2位出错而言,检1纠1的海明码并不能检验出来,下面让我们看看下一种海明码。
检2纠1海明码

相比较于检1纠1的海明码而言,检2纠1的海明码的区别在于,增加了一位总校验位的偶校验组合,用于对所有的校验码进行校验。

可以看到其海明码的生成,多了一个总校验位的生成。
对于海明码的检验则遵循如下的原则:

下面也来举个例子,来研究研究海明码的纠正过程吧。
假设对于带 8 位信息位的海明码在传送后,接收到的结果为1111001101011,其中有一位在传输过程中发生了位错,请检错并纠正。
首先,先找到各个校验位。
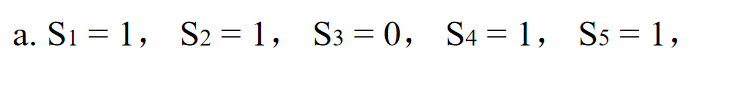
接着,按照上述校验规则,进行检验
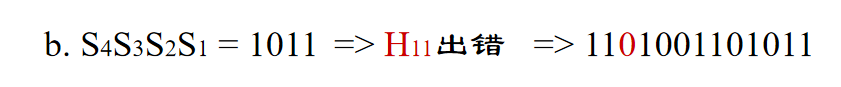
则纠正后的海明码为 1111001101011
CRC循环冗余码
二进制信息位流沿一条线逐位在部件之间或计算机之间传送称为串行传送。CRC(cyclic redundancy check)码可以发现并纠正信息存储或传送过程中连续出现的多位错误,因此在磁介质存储和计算机之间通信方面得到广泛应用。
CRC码一般是指k位信息码之后拼接r位校验位。应用CRC码的关键是如何从k位信息位简便地得到r位校验位(编码),以及如何从k+r位信息码判断是否出错。
下面,我们来具体看一看CRC循环冗余码的编码方式。
假设要发送的数据为 1101011011, 采用 CRC 的生成多项式为 P(X) = X4 + X + 1,求生成后的CRC循环校验码具体是多少?
首先,根据生成多项式,写出对应的二进制表达格式。
P(X) = X4 + 0X3 + 0X2 + X1 + X0 = 10011
接着,在数据位后面添0,对于生成多项式 10011,共有5位,故在数据位后面添加4个0。
11010110110000
接着利用新生成的11010110110000,生成余数。
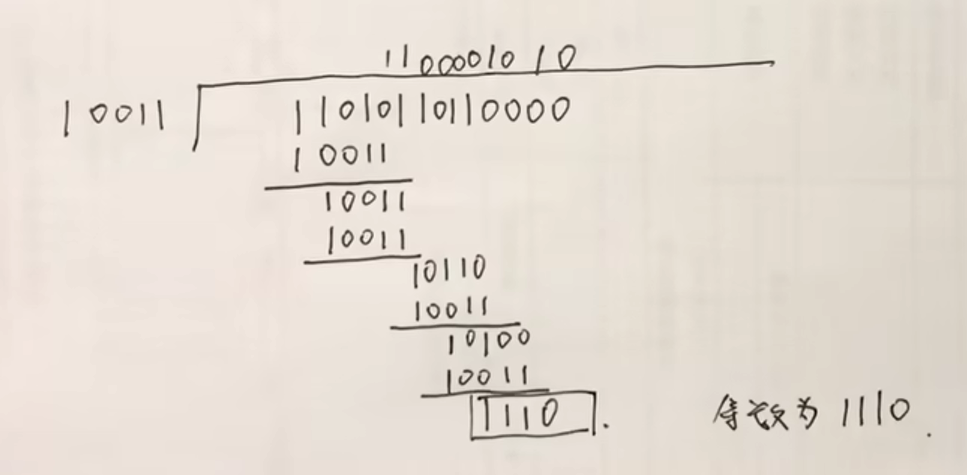
采用的是模2除法(异或),具体规则是先看高位,为1就上1,否则上0,然后进行模2减,也即异或操作。
最终,得到的CRC循环冗余码为 11010110111110
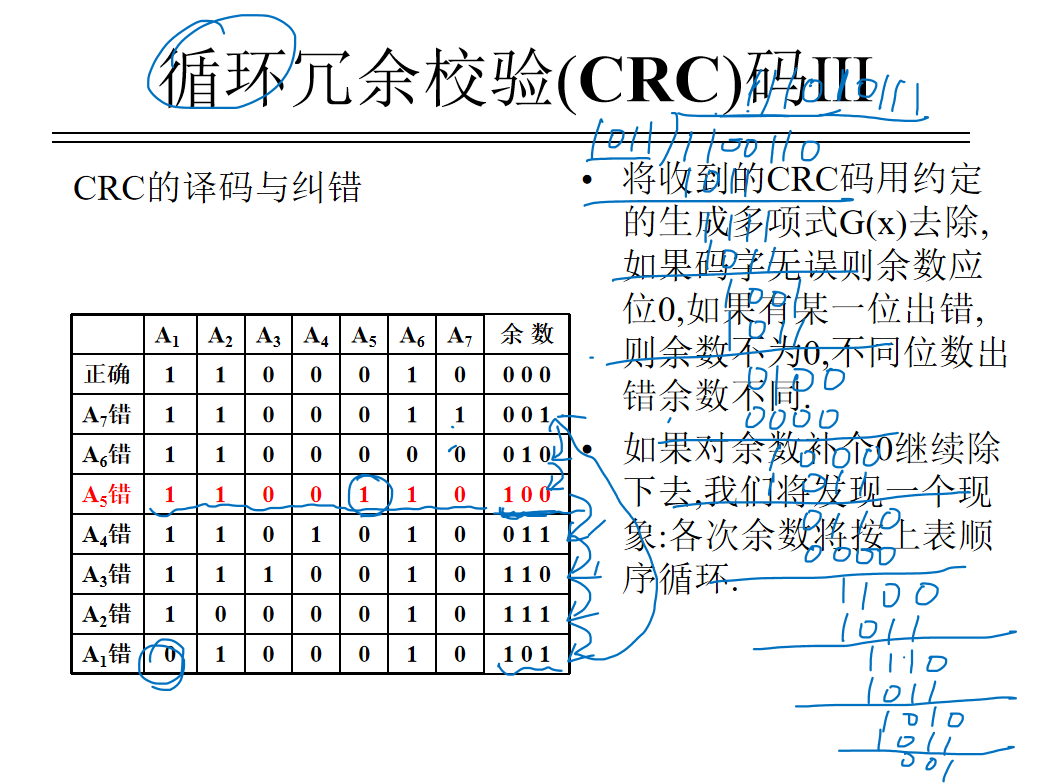
接收端进行校验时,具体就是将接收到的CRC循环冗余码去除以生成多项式。
若得到的余数结果为0,则认为传输无差错
若得到的余数结果不为0,则传输过程中出现了差错
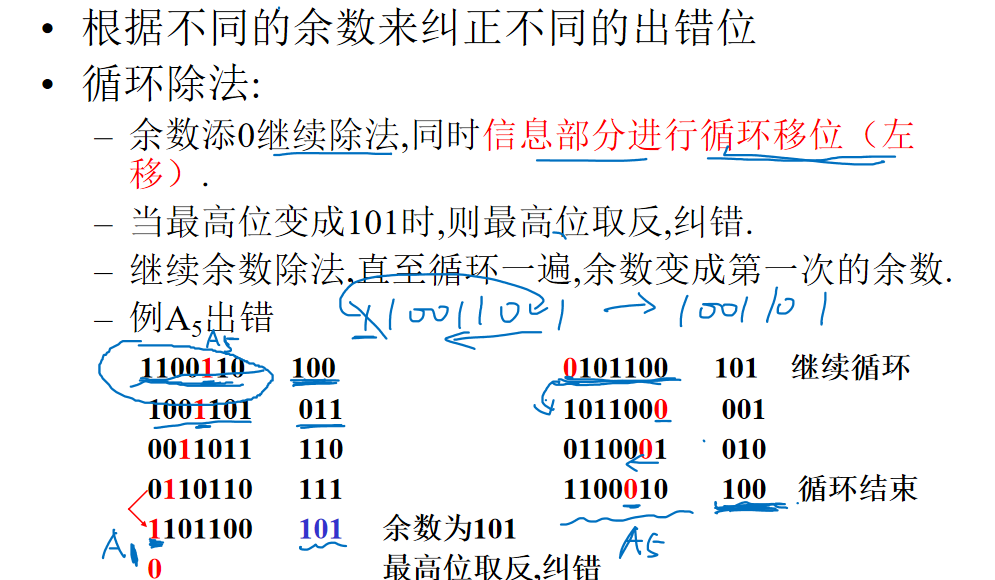
当余数结果不为0时,此时如果继续添加0,进行运算后,会发现得到的余数将构成一个循环。
例如,若正确的CRC循环冗余码为1100010000时,译码与纠错有如下:
小结


